Course overview

State machines — the fundamental concept used today in many practical applications, starting from UI programming in React, automated reply systems, lexical analysis in parsers and formal language theory — i.e. the RegExp machines, — and up to real life use cases, such as simple traffic lights, vending machines, and others.

The state machines are backed by the larger theoretical field of computer science known as Theory of Computation, and also by its direct theoretical model — the Automata Theory.

In this class we study the Automata Theory on the practical example of implementing a Regular Expressions machine.

See also: Essentials of Garbage Collectors class devoted to automatic memory management.

How to?

You can watch preview lectures, and also enroll to the full course, covering the aspects of Automata Theory and regular expressions in the animated and live-annotated format. See also details below what is in the course.

▶︎Enroll on Teachable ▶︎Enroll on Udemy

Available coupons: None at the moment

Why to take this class?

It’s not a secret, big tech companies, such as Google, Facebook, etc. organize their recruiting process around generalist engineers, which understand basic fundamental systems, data structures, and algorithms. In fact, it’s a known issue in tech-recruiting: there are a lot of “programmers”, but not so many “engineers”. And what does define an “engineer” in this case? — an ability so solve complex problems, with understanding (and experience) in those generic concepts.

And there is a simple trick how you can gain a great experience with transferable knowledge to other systems. — You take some complex theoretical field, which might not (yet) be related to your main job, and implement it in a language you’re familiar with. And while you build it, you learn all the different data structures and algorithms, which accommodate this system. It should specifically be something generic (for example, State machines), so you can further transfer this knowledge to your “day-to-day” job.

In this class we take this approach. To study Automata “Theory” we make it more practical: we take one of its widely-used applications, the lexical analysis, and pattern matching, and build a RegExp machine.

Not only we’ll completely understand how the Regular Expressions work under the hood (and what will make our usage of RegExp more professional), but also will be able to apply this knowledge about formal grammars, languages, finite automata — NFAs, DFAs, etc — in other fields of our work.

Who this class is for?

For any curious engineer willing to gain a generic knowledge about Finite Automata and Regular Expressions.

Notice though, that this class is not about how to use regular expressions (you should already know what a regular expression is, and actively use it on practice as a prerequisite for this class), but rather about how to implement the regular expressions — again with the goal to study generic complex system.

In addition, the lexical analysis (NFAs and DFAs specifically) is the basis for the parsers theory. So if you want to understand how parsers work (and more specifically, their Tokenizer or “Lexer” module), you can start here too. The path for a compiler engineer starts exactly from the Finite automata and lexical analyzer.

What are the features of this class?

The main features of these lectures are:

• Concise and straight to the point. Each lecture is self-contained, concise, and describes information directly related to the topic, not distracting on unrelated materials or talks.
• Animated presentation combined with live-editing notes. This makes understanding of the topics easier, and shows how (and when at time) the object structures are connected. Static slides simply don’t work for a complex content!

What is in the course?

The course is divided into three parts, in total of 16 lectures, and many sub-topics in each lecture. Below is the table of contents and curriculum.

Part 1: Formal grammars and Automata

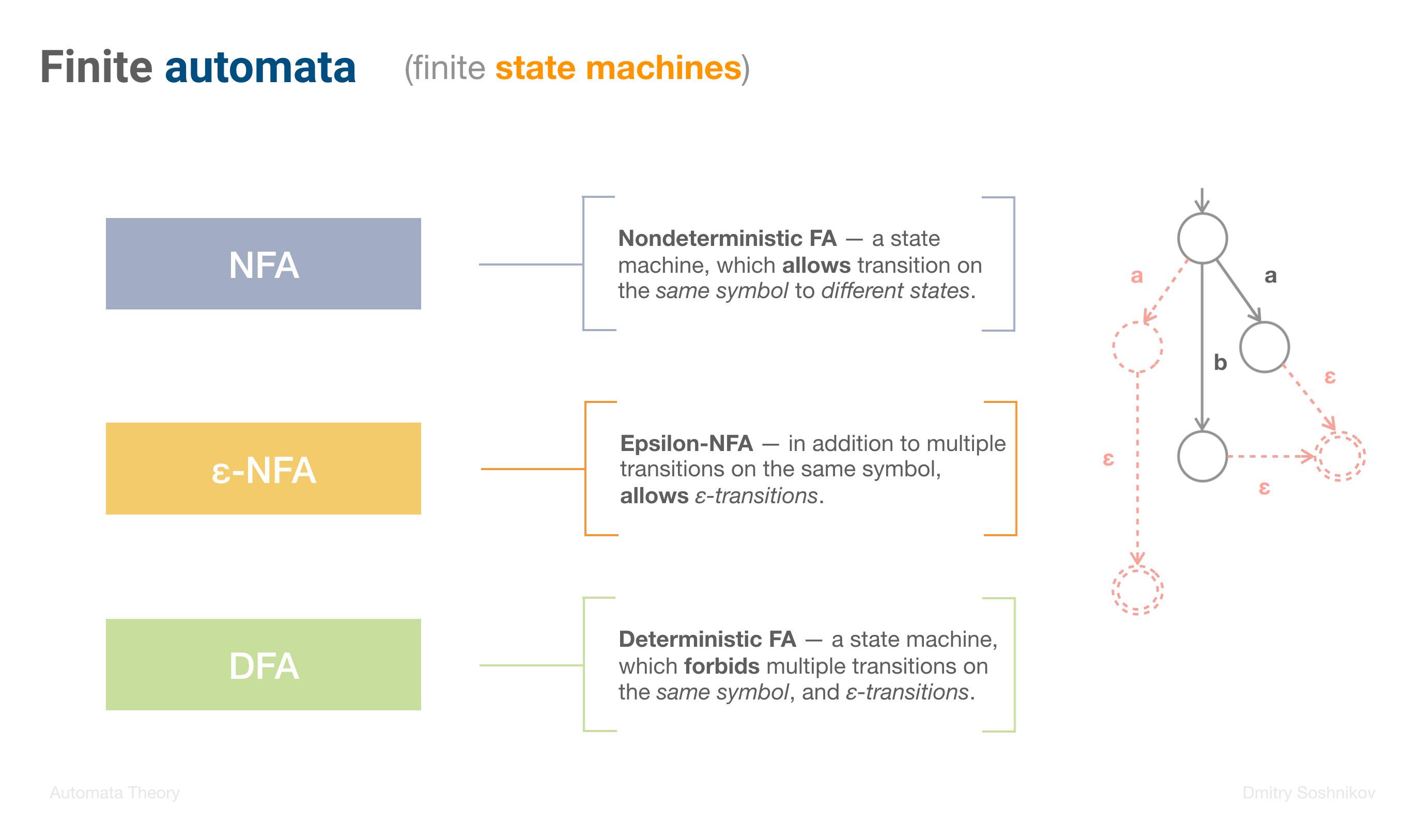
In this part we discuss the history of State machines, and Regular expressions, talk about Formal grammars in Language theory. We also consider different types of Finite automata, understanding the difference between NFA, ε-NFA, and DFA.

• Lecture 1: RegExp history

• Pioneers of formal grammars and regexp
• Stephen Kleene, Noam Chomsky, Ken Thompson
• Kleene-closure
• Regular grammars: Type 3
• Finite automata (State machines)
• NFA, DFA

• Lecture 2: Regular grammars

• Symbols, alphabets, languages
• Formal grammars: G = (N, T, P, S)
• Regular grammars: Type 3
• BNF notation vs. RegExp notation
• Right-linear grammars
• Nesting vs. Recursion
• Balanced parenthesis example
• Context-free grammars

• Lecture 3: Finite Automata

• From Regular grammars to State machines
• NFA, ε-NFA, DFA
• Epsilon-transitions
• Formal FA definition: (Q, Σ, Δ, q0, F)
• FA state implementation assignment

Part 2: RegExp NFA fragments

In this part we focus on the main NFA fragments, the basic building blocks used in RegExp automata. We study how by using generic principle of composition, we can obtain very complex machines, and also to optimize them.

• Lecture 4: Character and Epsilon NFA

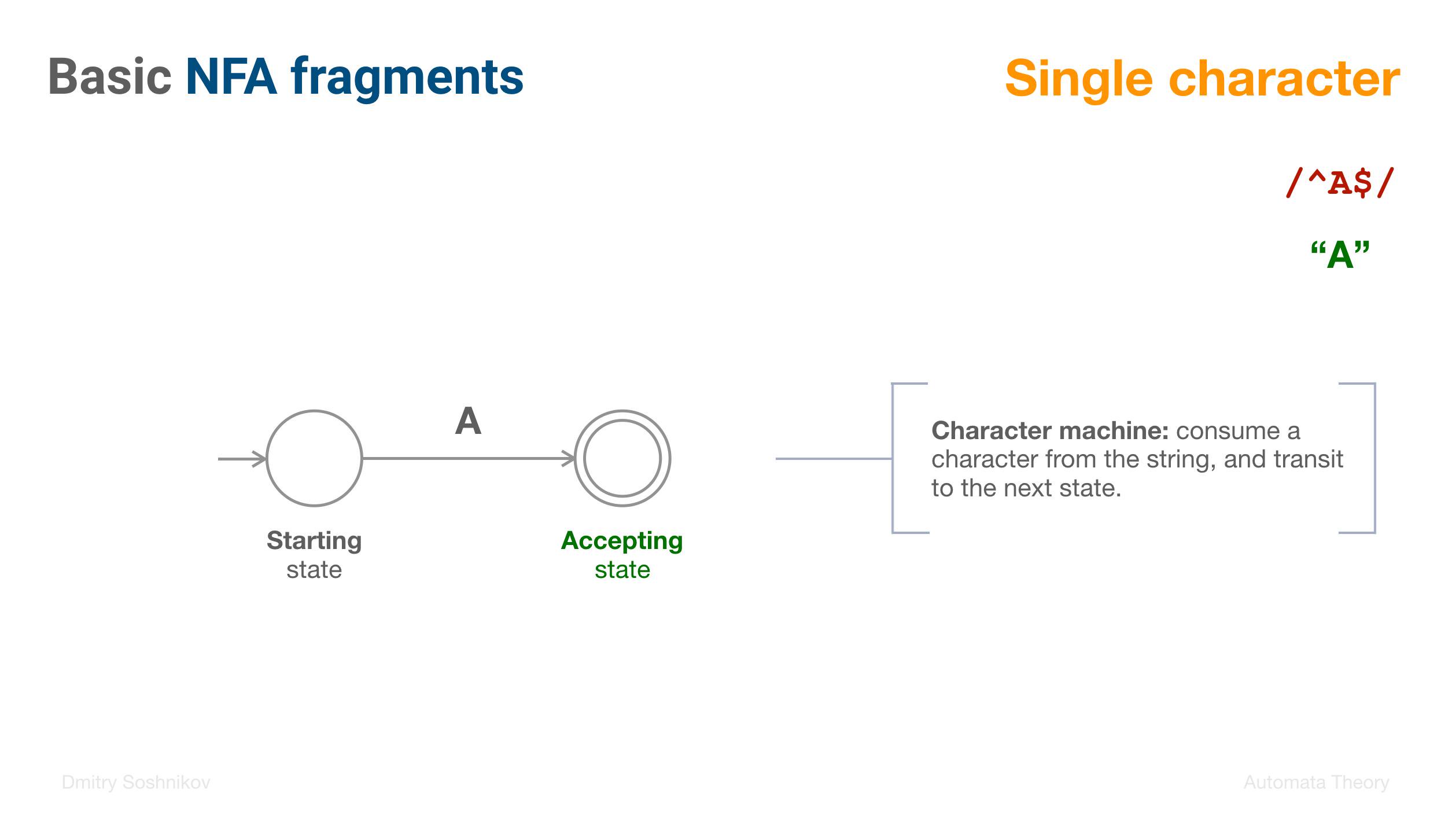
• NFA
• Single character fragment
• Epsilon fragment: “the empty string”

• Lecture 5: Concatenation pattern: AB

• Concatenation RegExp pattern: AB
• Machine as a Black-box
• Epsilon transition: attachment mechanism

• Lecture 6: Union pattern: A | B

• Union (aka Disjunction) pattern: A | B
• Epsilon transition: enter both machines
• Graph traversal

• Lecture 7: Kleene closure: A*

• Kleene-closure pattern: A*
• Repeat “zero or more” times
• 5 basic machines summary

• Lecture 8: Complex machines

• Patterns composition and decomposition
• Operator precedence
• Abstract syntax tree (AST)
• Recursive-descent interpreter
• Compound state machine

• Lecture 9: Syntactic sugar

• New syntax, same semantics
• Semantic rewrite to equivalent patterns
• A+, A?, Character classes
• NFA optimizations

• Lecture 10: NFA optimizations

• Preserve semantics, optimize implementation
• Optimized A* machine
• Specific A+ machine
• Specific A? machine
• Specific character class machine

Part 3: RegExp machine

Finally, we implement an actual test method of regular expressions which transit from state to state, matching a string. First we understand how an NFA acceptor works by traversing the graph. Then we transform it into an NFA table, and eventually to a DFA table. We also talk and describe in detail DFA minimization algorithm.

• Lecture 11: NFA acceptor

• NFA graph traversal
• Delegate implementation from machine to a state
• Epsilon-transitions: avoid infinite loops!
• RegExp test method implementation on NFAs

• Lecture 12: NFA table

• NFA graph to NFA table conversion
• Rows: states, Columns: alphabet
• Calculation of the Epsilon closure

• Lecture 13: RegExp-Tree tool

• RegExp analysis toolkit
• Parser API: obtain a RegExp AST
• NFA and DFA tables
• Optimizer module
• Transformation module

• Lecture 14: DFA table

• NFA to DFA conversion
• Subset Construction algorithm
• Multiple accepting states
• Epsilon closure: eliminate ε-transition

• Lecture 15: DFA minimization

• DFA graph
• States equivalence algorithm
• 0-N equivalence
• Merging states
• Minimal DFA graph

• Lecture 16: RegExp match

• RegExp pipeline
• RegExp test function implementation
• RegExp compilation: obtaining transition table
• Course overview
• Final notes

I hope you’ll enjoy the class, and will be glad to discuss any questions and suggestion in comments.